वेन आरेख

वेन आरेख (Venn diagram) वह आरेख हैं जो समुच्च्यों (या कुलकों) के परिमित संग्रहों (चीजों का समूह) के बीच सभी परिकाल्पनिक (आनुमानिक) रूप से संभव तार्किक संबंधों को दर्शाते हैं। वेन आरेख का आविष्कार 1880 के आसपास जॉन वेन द्वारा किया गया था। इनका कई क्षेत्रों में उपयोग किया जाता है, जैसे समुच्च्य सिद्धांत, प्रायिकता, तर्क, सांख्यिकी और कंप्यूटर विज्ञान।

उदाहरण के लिए, तीन समुच्चय A, B और C दिये हों, तो उनका वेन आरेख नीचे दर्शाया गया है-

$A=\{1,\,2,\,5\}$
$B=\{1,\,6\}$
$C=\{4,\,7\}$

ऋषभ साहू (अभय) :- समुच्चयों के बीच सम्बन्धों को आरेखों द्वारा निरूपित किया जा सकता है । किसी समुच्चय को संवृत ( बन्द ) वक्र के अन्दर बिन्दुओं द्वारा निरूपित करने का विचार सर्वप्रथम स्विस गणितज्ञ ऑयलर ( Euler ) ने दिया था । बाद में इस विचार को व्यवहार में अंग्रेज तर्कशास्त्री जॉन वेन ( 1834 - 1883 ) लाये । इसलिए समुच्चयों को निरूपित करने हेतु खींचे गए आरेखों को वेन आरेख कहते हैं । वेन आरेख में समष्टीय समुच्चय को एक आयत के अन्दर बिन्दुओं द्वारा तथा इसके उपसमुच्चयों को आयत के अन्दर संवृत वक्रों ( प्रायःवृत्त ) में बिन्दुओं द्वारा दर्शाया जाता है । यदि कोई समुच्चय A किसी समुच्चय B का उपसमुच्चय हो , तब A वाले वृत्त को B वाले वृत्त के अन्दर खींचा जाता है।

वेन आरेख

इसी प्रकार, ग्रीक वर्णमाला, लैटिन वर्णमाला, और रूसी वर्णमाला को तीन समुच्चय माना जाय, तो उनका वेन आरेख सामने दर्शाया गया है। इसमें देख सकते हैं कि कुछ वर्ण जो तीनों वर्णमालाओं में हैं, वे तीनों वृत्तों के सर्वनिष्ठ क्षेत्र में दिखाये गये हैं।

परिचय

वेन आरेख द्वारा समुच्चयों का आपसी सम्बन्ध दिखाया जा सकता है तथा उसमें समुच्चयों का प्रतिच्छेद (इन्टर्सेक्शन), संघ (युनियन) तथा वियोजन (disjunction) दिखा सकते हैं।

प्रतिच्छेद

A = {1; 2; 3; 4; 6; 12}
B = {1; 3; 5; 15}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}

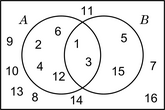
संघ

A = {1; 2; 3; 4; 6; 12}
B = {1; 2; 3; 6}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}

वियोजन

A = {2; 4; 6; 8}
B = {1; 3; 5; 7; 9}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
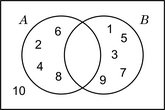